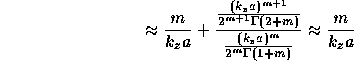Stability of a Cylindrical Plasma

Above we talked about the equilibrium and stability of a plasma in a magnetic field without plasma current. A plasma can be confined by a field induced by currents passing through the plasma. At a high current level, the magnetic field induced by it is sufficient enough to ensure stability. This is called pinch effect. A linear discharge confined by the current field is called a linear or zeta pinch. In this section we are going to discuss a cylindrical plasma system.
Assume current distribution and pressure distribution are: 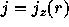, p=p(r).
The magnetic field induced by the current: 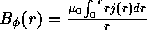(80)
At the plasma boundary, 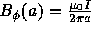(81)
Outside of the plasma, 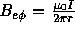(82)
The equation of plasma equilibrium can be written as :
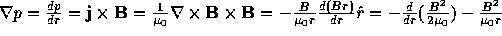(83)
The first term yields the magnetic pressure gradient and the second, the force associated with the tension of the lines of force. The integral condition of equilibrium is found by multiplying above by and integrating over 0 to a. Then we get: left side

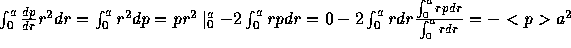
right side: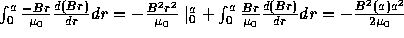
left side=right side 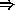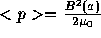(84)
The above result shows that when the plasma density or temperature increases, the plasma current need to increase accordingly.
In skin pinch (where the current flows on the plasma surface), as j=B=0 in the plasam, then the plasma pressure is constant in the plasma. At the boundary .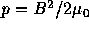
In uniform current case, from eq.(80) 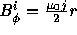, therefore from eq.(83) the pressure distribution is parabolic: (85)
where
In case there exist a longitudinal magnetic field 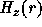inside and outside of the plasma. Then the equilibrium condition eq.(84) is modified by:
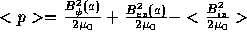(86)
II. Stability Problems

Let us now discuss the development of some typical instabilities of a current carrying plasma column.
Sausage Instability: 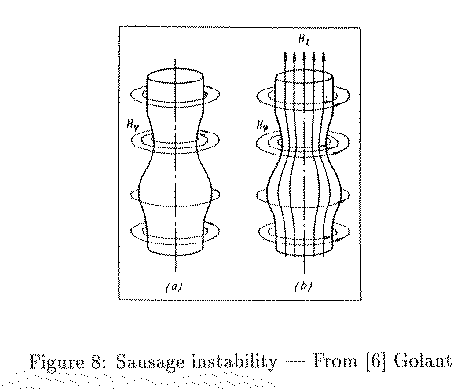See fig.8a, is a kind of flute instability. Local narrowing of the cross section will accelerate narrowing process because of local growth of magnetic field. This instability may result in a complete discontinuity of the current at the neck. With external longitudinal magnetic field, this kind of instability can be suppressed by the magnetic tention force.(Small k See fig.8b.
Kink Instability: See fig.9a, is mode=1 kink instability. This kind of instability also caused by the local bending of the plasma column, which will increase current induced magnetic field at one side and decrease it at the other side. Thus cause the column to bend more. Such kind of instability can be reduced by adding an external homogeneous magnetic field like above.
Obviously, only those perturbations with small wavelength can be effectively suppressed by adding longitudinal field. For long wavelength, magentic tension force will not strong enough to interfere with the plasma bending. To suppress this, a thick conductor wall is used. See fig.9b. As long as the perturbation process is much faster than magnetic penetrating time, the wall will promote the suppression of bending.
Skin Current Model

We'll analyze instability problem of a plasma column by assuming that there is only skin current exist. So 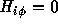. Outside the plasma the magnetic region is bounded by the casing (r=b, See fig.9b). Since the equilibrium condistions are independent of 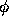and z, the displacement can be written as
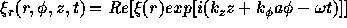(87) Since 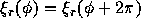, therefore, , where m is called mode of oscillation. See fig.10 for view of different values of m.
The soulution of linearized euation of MHD (eq.(41)) with certain boundary condiftions leads to a dispersion relation similar to eq.(66):

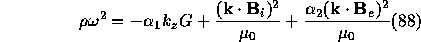
where 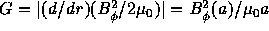(See eq.(82)) is an effective force acting on the plasma surface. The coefficient and 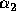are equal to:

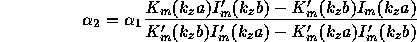
where and 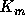are modified m-order Bessel functions. We'll use above results to get Kruskal-Shafranov criterion.
In a magnetic confined plasma with a strong longitudinal magnetic field, stability condition can be carried out by using eq.(88). Assume at the boundary 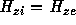, we have

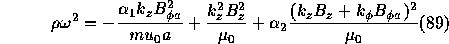
Since only 1st term is negative and 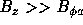, only long-wave perturbation with 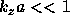can obviously unstable. At ,

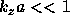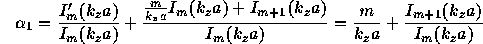
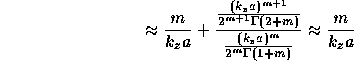
Same 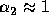, and the dispersion equation takes the form ( )

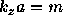It's easy to see that only perturbations with m=1 can be unstable. Therefore,

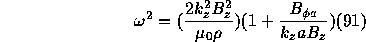
It is seen that the plasma boundary is unstable to a screw-type instability with m=1 mode, provided 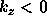and
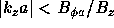(92)
This is used to determine the minimum perturbation wavelength
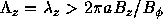(93)
where 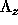is the pitch of the helical plasma column.
On the other hand, the wavelength is usually limited by the plasma column length L. In accordance with eq.(93), the instability criterion can be written as:
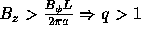(94)
where q is safty-factor. This is called Kruskal-Shafranov criterion.
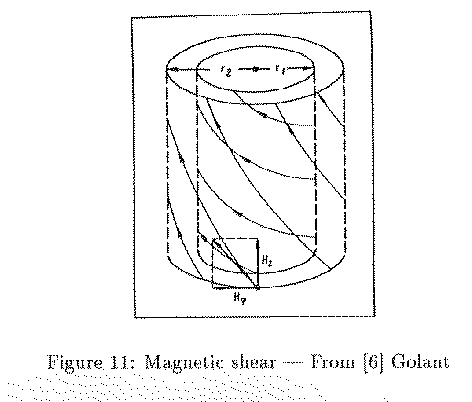
Above discussion is based on skinned-current model. Analysis of stability for a plasma cylinder with a distributed current is much more complicated. They ar largely determined by the shear in the plasma volume. For instance, for perturbations with a large m, a sufficient stability criterion can be represented as

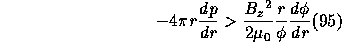
This is called Sydem criterion, where 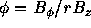gives azimuthal angle change per longitudinal unit length, and 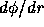characterizes the shear. (See fig.11)